
この記事では、平方根の計算について書いています。
大部分は中学数学と重複する内容ですので、高校生の皆様は適宜読み飛ばして進めてください。
なお、平方根の何たるかが不安な人は先にこちらの記事からチェックされることをおすすめします。
平方根の計算は大きく分けて「乗除」と「加減」の\(\,2\,\)種類です。
それぞれの計算方法を区別して説明していきます。
平方根の乗除
乗除とは、掛け算と割り算です。
平方根の計算において、掛け算と割り算はルートの中同士で計算することができます。
たとえば...
\(\sqrt{2}\times\sqrt{3}=\sqrt{2\times 3}=\sqrt{6}\)
このような計算が認められます。
平方根のおおよその値を用いて確認しておくと...
- \(\sqrt{2}=1.41421356\,\cdots\) (一夜一夜に人見ごろ)
- \(\sqrt{3}=1.7320508\,\cdots\) (人並みにおごれや)
- \(\sqrt{6}=2.4494897\,\cdots\) (煮よよく弱くな)

\(\sqrt{2}\times\sqrt{3}=1.41421356\times 1.7320508\,\)としたとき、計算結果は\(\,\sqrt{6}\,\)の値にほぼ等しいことが確かめられました。
この話をまとめておくと...
\(x>0,~y>0\,\)のとき
\(\sqrt{x}\times\sqrt{y}=\sqrt{xy}\)
\(\sqrt{x}\div\sqrt{y}=\sqrt{\displaystyle\frac{x}{y}}\)
また、平方根の乗除は基本的にルートの中同士と外同士で行います。
たとえば...
\(2\times\sqrt{3}=2\sqrt{3}\)
\(2\sqrt{3}\times 4\sqrt{5}=2\times4\sqrt{3\times 5}=8\sqrt{15}\)
計算方法も大切ですが、\(x\sqrt{y}=x\times\sqrt{y}\,\)という意味も大切です。
平方根の加減
加減とは、足し算と引き算です。
平方根の計算において、足し算と引き算はルートの中同士で計算することができません。
\(\sqrt{2}+\sqrt{3}\neq\sqrt{2+3}=\sqrt{5}\)
このような計算は認められていません。
平方根のおおよその値を用いて確認しておくと...
- \(\sqrt{2}=1.41421356\,\cdots\) (一夜一夜に人見ごろ)
- \(\sqrt{3}=1.7320508\,\cdots\) (人並みにおごれや)
- \(\sqrt{5}=2.2360679\,\cdots\) (富士山麓オウム鳴く)
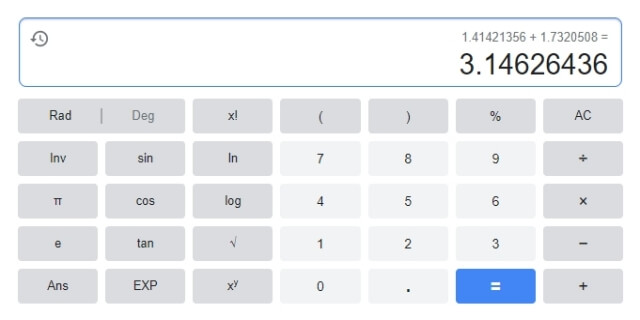
\(\sqrt{2}+\sqrt{3}=1.41421356+1.7320508\,\)としたとき、計算結果は\(\,\sqrt{5}\,\)の値に等しくないことが確かめられました。
少し違和感を感じるかもしれませんが、この形はこれ以上簡単にすることができません。
逆に言えば、何らかの問題で計算結果が\(\,\sqrt{2}+\sqrt{3}\,\)となった場合、そのまま答えとしても構わないということです。
ただし、以下のような計算は認められています。
\(\sqrt{2}+\sqrt{2}=2\sqrt{2}\)
\(1.41421356+1.41421356=2\times 1.41421356\,\)は当然成り立ちますよね。
つまり、平方根の加減は...
- ルートの中身が揃っている場合は係数同士を合わせることができる
- ルートの中身が揃っていない場合は計算できない
ということです。
練習問題
それでは、ここまで書いたことを練習問題を通じて確認していきましょう。
(問) 次の計算をせよ。
(1) \(\sqrt{2}\times\sqrt{6}\)
(2) \(\sqrt{3}\div\sqrt{6}\)
(3) \(7\sqrt{3}-5\sqrt{3}\)
(4) \(\sqrt{12}+\sqrt{45}\)
(1) \(\sqrt{2}\times\sqrt{6}\)
この問題は掛け算なので、ルートの中同士で計算を行うことができます。
\(\sqrt{2}\times\sqrt{6}=\sqrt{2\times6}=\sqrt{12}\)
しかし、\(\sqrt{12}\,\)のままでは不正解です。
平方根を変形できる場合は必ずその処理を行わなければなりません。
よって...
\(\sqrt{2}\times\sqrt{6}=\sqrt{12}=2\sqrt{3}\)
これが答えです。
(2) \(\sqrt{3}\div\sqrt{6}\)
この問題は割り算なので、(1)と同様にルートの中同士で計算を行うことができます。
\(\sqrt{3}\div\sqrt{6}=\sqrt{\displaystyle\frac{3}{6}}=\sqrt{\displaystyle\frac{1}{2}}\)
しかし、この問題も\(\,\sqrt{\displaystyle\frac{1}{2}}\,\)のままでは不正解です(正解になる場合もあります)。
まず、分数全体にかぶさったルートを分子分母に分割します。
\(\sqrt{\displaystyle\frac{x}{y}}=\displaystyle\frac{\sqrt{x}}{\sqrt{y}}\,\)という変形はよく使われるので、押さえておいてくださいね。
\(\sqrt{3}\div\sqrt{6}=\sqrt{\displaystyle\frac{1}{2}}=\displaystyle\frac{\sqrt{1}}{\sqrt{2}}=\displaystyle\frac{1}{\sqrt{2}}\)
そして、分母の有理化を行います。
よって...
\(\sqrt{3}\div\sqrt{6}=\displaystyle\frac{1}{\sqrt{2}}=\displaystyle\frac{\sqrt{2}}{2}\)
これが答えです。
(3) \(7\sqrt{3}-5\sqrt{3}\)
この問題は引き算なので、ルートの中同士で計算を行うことはできません。
しかし、ルートの中身が揃っているので、係数同士を合わせることができます。
よって...
\(7\sqrt{3}-5\sqrt{3}=2\sqrt{3}\)
これが答えです。
イメージとしては文字式の計算\(\,7x-5x=2x\,\)と同じように考えて構いません。
(4) \(\sqrt{20}+\sqrt{45}\)
この問題は足し算なので、ルートの中同士で計算を行うことはできません。
また、ルートの中身も揃っていないので、計算のしようがないようにも見えます。
しかし、平方根を変形すれば、ルートの中身を揃えることができます。
\(\sqrt{20}=2\sqrt{5}\)
\(\sqrt{45}=3\sqrt{5}\)
よって...
\(\sqrt{20}+\sqrt{45}=2\sqrt{5}+3\sqrt{5}=5\sqrt{5}\)
これが答えです。
まとめ
平方根の乗除はルートの中同士計算できる。
平方根の加減はルートの中同士計算できない。
その他の細かい点にも触れましたが、一番大切なのはこれです。
確実に押さえた上で、各種問題にチャレンジしてください。

