三角比の定義 | 直角三角形による定義【数学I】

この記事では、三角比の定義について書いています。

\(\sin\,\)(サイン)、\(\cos\,\)(コサイン)、\(\tan\,\)(タンジェント)

\(\,3\,\)つの謎めいたものが高校数学の序盤で突如として現れ、苦戦する人が非常に多いです。

以下では、三角比の定義(直角三角形による定義)を分かりやすく説明していますので、最後まで読んで正しく覚えてください。

三角比の定義

三角比とは、直角三角形の辺の比を表したものです。

どの辺とどの辺の比かというと...

まず、角\(\,\theta\,\)(シータ)を左下、直角を右下に配置します。

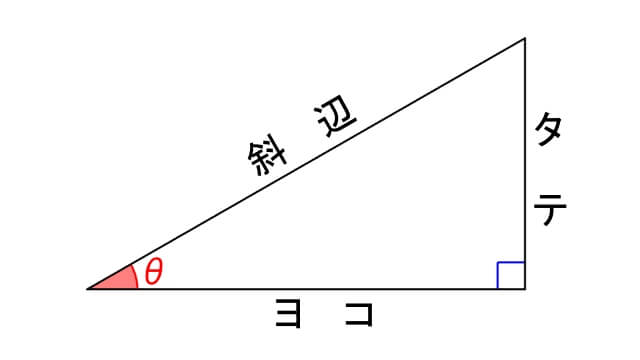
このポジショニングはとても大切です。

そして、このとき...

これが三角比の定義です。

最初はこの定義を覚えるところからスタートしてください。

sinって何だよ！？

そう思う気持ちもわかりますが、とにかく定義を覚えるしかありません。

例題

では、例題を通して確認しておきましょう。

各辺において以下の式が成り立つので...

\(5^{\,2}=4^{\,2}+3^{\,2}\)

三平方の定理の逆より、△\({\rm ABC}\,\)は直角三角形です。

よって、三角比の定義からすべての値が求められます。

三角比を求めたい角を左下、直角を右下に配置すると...

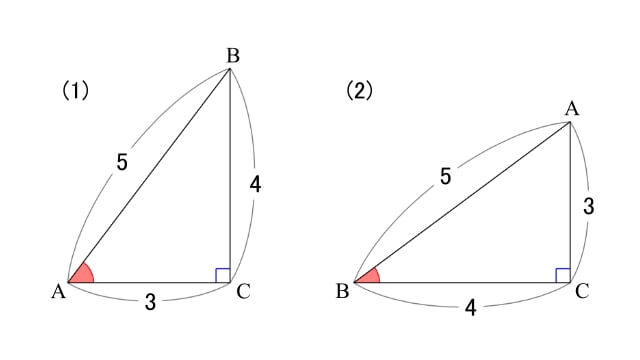
図より

(1)　\(\sin{\rm A}=\displaystyle\frac{4}{5}\)　\(\cos{\rm A}=\displaystyle\frac{3}{5}\)　\(\tan{\rm A}=\displaystyle\frac{4}{3}\)

(2)　\(\sin{\rm B}=\displaystyle\frac{3}{5}\)　\(\cos{\rm B}=\displaystyle\frac{4}{5}\)　\(\tan{\rm B}=\displaystyle\frac{3}{4}\)

なお、角の配置の仕方にはくれぐれも注意してください。

有名角の三角比

さて、直角三角形といえば、三角定規の辺の比を中学数学で覚えたはずです。

\(30^{\circ}\)、\(60^{\circ}\)、\(90^{\circ}\)の三角形は\(\,1:2:\sqrt{3}\)

\(45^{\circ}\)、\(45^{\circ}\)、\(90^{\circ}\)の三角形は\(\,1:1:\sqrt{2}\)

でしたね。

ここで、三角比を求めたい角度を左下、直角を右下に置くと...

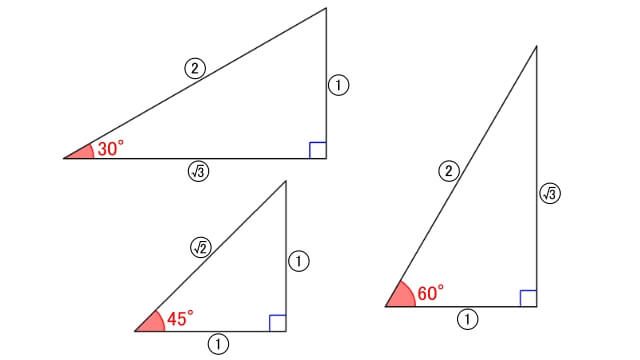
図より

\(\sin30^{\circ}=\displaystyle\frac{1}{2}\)　\(\cos30^{\circ}=\displaystyle\frac{\sqrt{3}}{2}\)　\(\tan30^{\circ}=\displaystyle\frac{1}{\sqrt{3}}\)

\(\sin45^{\circ}=\displaystyle\frac{1}{\sqrt{2}}\)　\(\cos45^{\circ}=\displaystyle\frac{1}{\sqrt{2}}\)　\(\tan45^{\circ}=1\)

\(\sin60^{\circ}=\displaystyle\frac{\sqrt{3}}{2}\)　\(\cos60^{\circ}=\displaystyle\frac{1}{2}\)　\(\tan60^{\circ}=\sqrt{3}\)

これらの値は図を書いて考えればわかることですが、有名角の三角比として暗記しておいてください。

念のため、表にまとめておきます。

もう一度言いますが、必ず暗記してください。

これらの値はこの先の学習で三角比を扱う際に当然のように登場します。

まとめ

直角三角形において、角\(\,\theta\,\)を左下、直角を右下に配置したとき

\(\sin\theta=\displaystyle\frac{\bf タテ}{\bf 斜辺}\)　\(\cos\theta=\displaystyle\frac{\bf ヨコ}{\bf 斜辺}\)　\(\tan\theta=\displaystyle\frac{\bf タテ}{\bf ヨコ}\)

これが三角比の定義(直角三角形による定義)です。

特に、\(30^{\circ}\)、\(45^{\circ}\)、\(60^{\circ}\)の三角比は暗記しておいてください。