
この記事では、三角比の拡張について書いています。
三角比を初めて学習した際、大抵の人は直角三角形による定義で説明を受けたはずです。
この定義が間違っているということは決してありませんが、これでは\(\,90^{\circ}\,\)までの角度しか三角比を定義することができません。
そこで、三角比を拡張するべく、単位円による定義が新たに導入されます。
以下では、単位円による三角比の定義について図をたくさん取り入れて丁寧に説明していますので、最後まで読んでもらえると嬉しいです。
目次
三角比の定義
直角三角形による定義
まずは、直角三角形による三角比の定義を復習しておきます。
角\(\,\theta\,\)を左下、直角を右下に配置したとき
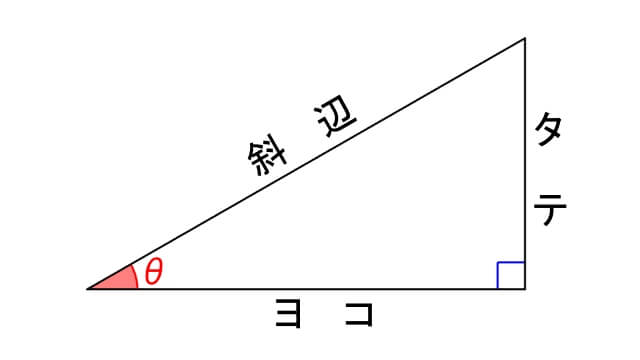
それぞれをこのように定義するのでしたね。
なお、直角三角形による定義が不安な人は先にこちらの記事からチェックされることをおすすめします。
とはいえ、この定義の仕方では、直角三角形の内部に配置できる角度(\(\,0^{\circ}<\theta<90^{\circ}\,\))しか三角比を定義することができません。
単位円による定義
座標平面上で、原点\(\,{\rm O}\,\)中心、半径\(\,1\,\)の円を単位円といいます。
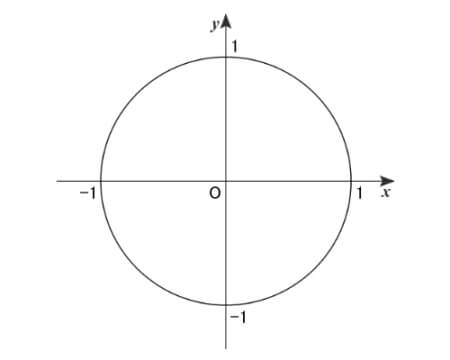
この単位円周上に任意の点\(\,{\rm P}\,\)をとります。
ここで、\({\rm OP}\,\)と\(\,x\,\)軸の正の向きとの成す角を\(\,\theta\,\)とするとき
点\(\,{\rm P}\,\)の\(\,x\,\)座標を\(\,\cos\theta\,\)、\(y\,\)座標を\(\,\sin\theta\,\)、\({\rm OP}\,\)の傾きを\(\,\tan\theta\,\)と定義します。
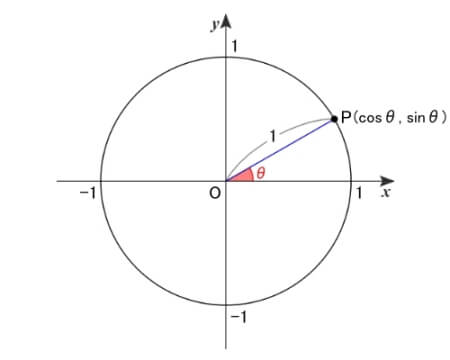
これが単位円による三角比の定義です。
このように定義することで、\(0^{\circ}\,\)や\(\,90^{\circ}\,\)以上の角度の三角比も定義することができるようになります。
ちなみに、数学Iの範囲では\(\,180^{\circ}\,\)までの角度しか扱いませんので、ひとまず安心しておいてください。
有名角の三角比
さて、直角三角形による定義において、\(30^{\circ}\,\)、\(45^{\circ}\,\)、\(60^{\circ}\,\)の三角比は有名角の三角比として暗記したはずです。
ここでは、有名角の三角比も拡張していきますね。
30°、150°の三角比
30°について
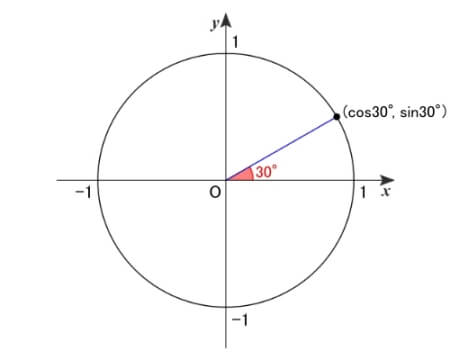
単位円による定義より、この点の座標から\(\,30^{\circ}\,\)の三角比の値が求められます。
この点から\(\,x\,\)軸に垂線を下ろして直角三角形を作ると...
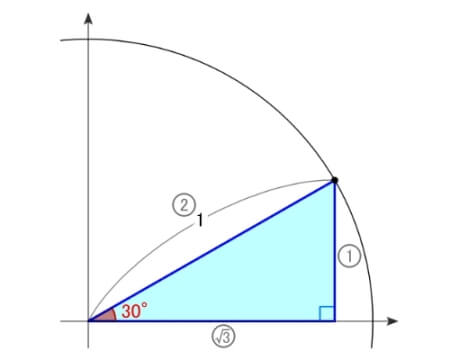
直角三角形の
ヨコの長さが\(\,x\,\)座標、つまり、\(\cos30^{\circ}\,\)の値
タテの長さが\(\,y\,\)座標、つまり、\(\sin30^{\circ}\,\)の値
タテをヨコで割った斜辺の傾きが\(\,\tan30^{\circ}\,\)の値
ですね。
三角定規の辺の比(\(\,1:2:\sqrt{3}\,\))より
ヨコは\(\,\displaystyle\frac{1}{2}\,\)、タテは\(\,\displaystyle\frac{\sqrt{3}}{2}\,\)、傾きは\(\,\displaystyle\frac{1}{\sqrt{3}}\,\)になります。
よって、\(\sin30^{\circ}=\displaystyle\frac{1}{2}\) \(\cos30^{\circ}=\displaystyle\frac{\sqrt{3}}{2}\) \(\tan30^{\circ}=\displaystyle\frac{1}{\sqrt{3}}\)
当然ですが、単位円による定義でも直角三角形による定義でも、三角比の値が変わることはありません。
150°について

もしかすると、\(30^{\circ}\,\)と\(\,150^{\circ}\,\)をなぜ一緒に扱うのかと疑問に感じた人もいるかもしれませんが、その理由は単純です。
\(150^{\circ}\,\)は単位円の半周分にあたる\(\,180^{\circ}\,\)から\(\,30^{\circ}\,\)戻ったところに位置しています。
以下のように合同な直角三角形を作ると...
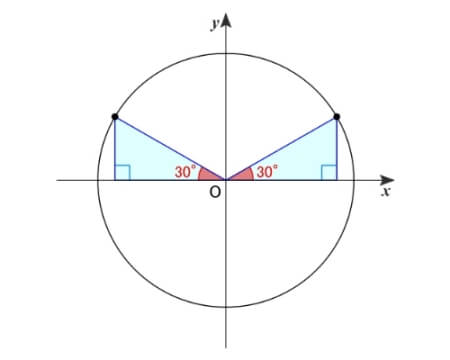
図より、\(\,y\,\)座標は\(\,\sin30^{\circ}\,\)の値に等しく、\(\,x\,\)座標と傾きはそれぞれ\(\,\cos30^{\circ}\,\)と\(\,\tan30^{\circ}\,\)の逆符号の値です。
よって、\(\sin150^{\circ}=\displaystyle\frac{1}{2}\) \(\cos150^{\circ}=-\displaystyle\frac{\sqrt{3}}{2}\) \(\tan150^{\circ}=-\displaystyle\frac{1}{\sqrt{3}}\)
鈍角の三角比の値を求める際は\(180^{\circ}\,\)から何度戻った角度であるかを考えることが大切です。
45°、135°の三角比
45°について
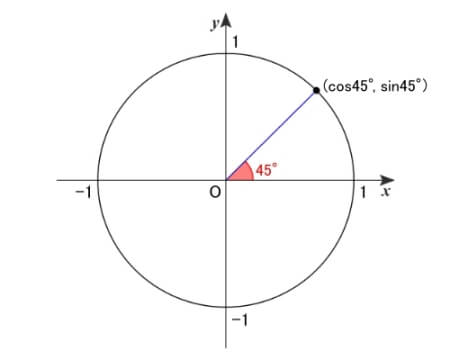
\(\,45^{\circ}\,\)の三角比の値も同様の手順で求められます。
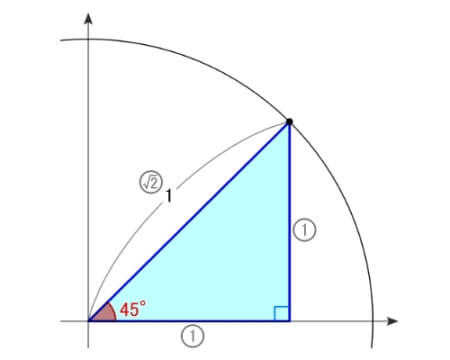
直角三角形の
ヨコの長さが\(\,x\,\)座標、つまり、\(\cos45^{\circ}\,\)の値
タテの長さが\(\,y\,\)座標、つまり、\(\sin45^{\circ}\,\)の値
タテをヨコで割った斜辺の傾きが\(\,\tan45^{\circ}\,\)の値
ですね。
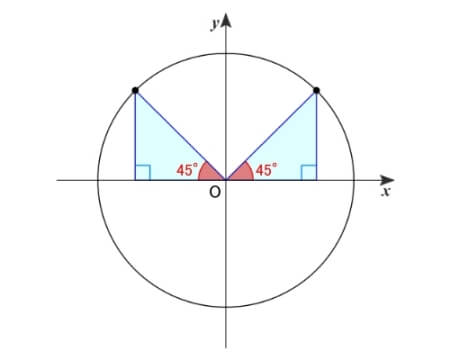
三角定規の辺の比(\(\,1:1:\sqrt{2}\,\))より、ヨコは\(\,\displaystyle\frac{1}{\sqrt{2}}\,\)、タテは\(\,\displaystyle\frac{1}{\sqrt{2}}\,\)、傾きは\(\,1\,\)
よって、\(\sin45^{\circ}=\displaystyle\frac{1}{\sqrt{2}}\) \(\cos45^{\circ}=\displaystyle\frac{1}{\sqrt{2}}\) \(\tan45^{\circ}=1\)
135°について
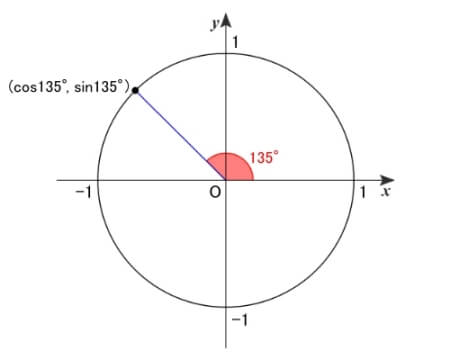
\(135^{\circ}\,\)は\(\,180^{\circ}\,\)から\(\,45^{\circ}\,\)戻ったところに位置しているので...
図より、\(\,y\,\)座標は\(\,\sin45^{\circ}\,\)の値に等しく、\(\,x\,\)座標と傾きはそれぞれ\(\,\cos45^{\circ}\,\)と\(\,\tan45^{\circ}\,\)の逆符号の値
よって、\(\sin135^{\circ}=\displaystyle\frac{1}{\sqrt{2}}\) \(\cos135^{\circ}=-\displaystyle\frac{1}{\sqrt{2}}\) \(\tan135^{\circ}=-1\)
60°、120°の三角比
60°について
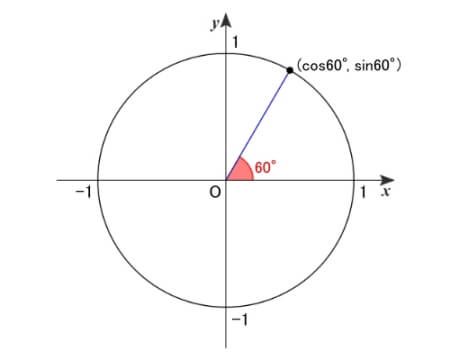
\(\,60^{\circ}\,\)の三角比の値も同様の手順で求められます。
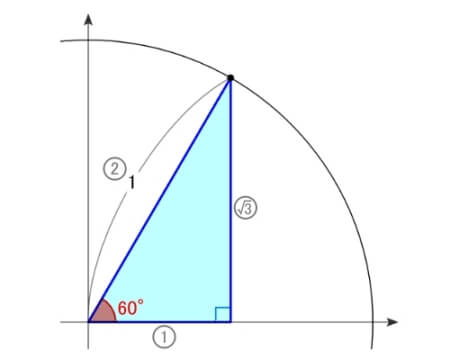
直角三角形の
ヨコの長さが\(\,x\,\)座標、つまり、\(\cos60^{\circ}\,\)の値
タテの長さが\(\,y\,\)座標、つまり、\(\sin60^{\circ}\,\)の値
タテをヨコで割った斜辺の傾きが\(\,\tan60^{\circ}\,\)の値
ですね。
三角定規の辺の比(\(\,1:2:\sqrt{3}\,\))より、ヨコは\(\,\displaystyle\frac{1}{2}\,\)、タテは\(\,\displaystyle\frac{\sqrt{3}}{2}\,\)、傾きは\(\,\sqrt{3}\,\)
よって、\(\sin60^{\circ}=\displaystyle\frac{\sqrt{3}}{2}\) \(\cos60^{\circ}=\displaystyle\frac{1}{2}\) \(\tan60^{\circ}=\sqrt{3}\)
120°について

\(120^{\circ}\,\)は\(\,180^{\circ}\,\)から\(\,60^{\circ}\,\)戻ったところに位置しているので...
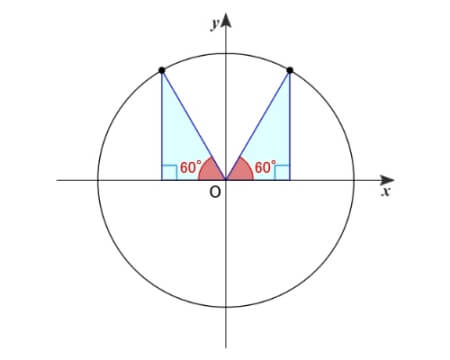
図より、\(\,y\,\)座標は\(\,\sin60^{\circ}\,\)の値に等しく、\(\,x\,\)座標と傾きはそれぞれ\(\,\cos60^{\circ}\,\)と\(\,\tan60^{\circ}\,\)の逆符号の値
よって、\(\sin120^{\circ}=\displaystyle\frac{\sqrt{3}}{2}\) \(\cos120^{\circ}=-\displaystyle\frac{1}{2}\) \(\tan120^{\circ}=-\sqrt{3}\)
0°、90°、180°の三角比
0°について
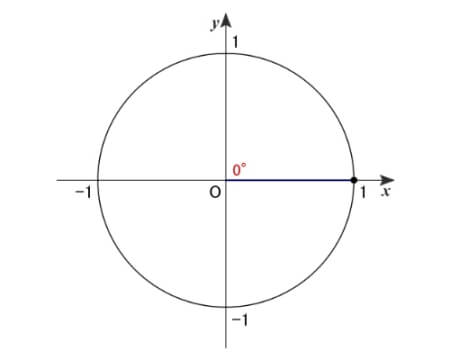
この点の座標\(\,(1,~0)\,\)がそれぞれ\(\,\cos0^{\circ}\,\)と\(\,\sin0^{\circ}\,\)の値です。
また、\(\sin0^{\circ}\,\)を\(\,\cos0^{\circ}\,\)で割って\(\,\tan0^{\circ}\,\)の値が求められます。
よって、\(\sin0^{\circ}=0\) \(\cos0^{\circ}=1\) \(\tan0^{\circ}=0\)
90°について

この点の座標\(\,(0,~1)\,\)がそれぞれ\(\,\cos90^{\circ}\,\)と\(\,\sin90^{\circ}\,\)の値です。
また、\(\sin90^{\circ}\,\)を\(\,\cos90^{\circ}\,\)で割って\(\,\tan90^{\circ}\,\)を求めたいところですが、\(\,\cos90^{\circ}\,\)の値が\(\,0\,\)なので\(\,\tan90^{\circ}\,\)は定義することができません。
数学のルールとして、\(0\,\)で割ることは認められていないのでしたね。
よって、\(\sin90^{\circ}=0\) \(\cos90^{\circ}=1\) \(\tan90^{\circ}\,\)は定義しない
180°について
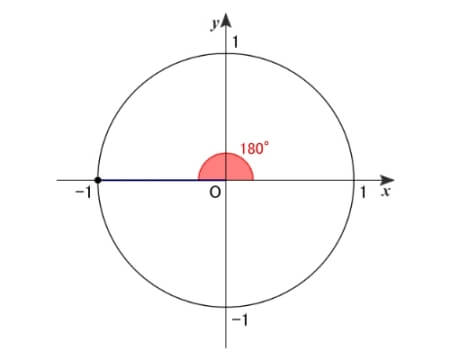
この点の座標\(\,(-1,~0)\,\)がそれぞれ\(\,\cos180^{\circ}\,\)と\(\,\sin180^{\circ}\,\)の値です。
また、\(\sin180^{\circ}\,\)を\(\,\cos180^{\circ}\,\)で割って\(\,\tan180^{\circ}\,\)の値が求められます。
よって、\(\sin180^{\circ}=0\) \(\cos180^{\circ}=-1\) \(\tan180^{\circ}=0\)
まとめ
単位円による定義より、\(0^{\circ}\,\)や\(\,90^{\circ}\,\)以上の角度の三角比も定義することができるようになります。
有名角の三角比の値を表にまとめると...

単位円周上の点の座標を考えること、鈍角の三角比は\(180^{\circ}\,\)から何度戻った角度であるかを考えること、この2つが大切です。
また、鈍角の三角比は\(\,\sin\,\)の値は正ですが、\(\cos\,\)と\(\,\tan\,\)の値は負になります。
少し複雑な話もありましたが、これらのことをしっかりと押さえておいてください。

